 |
Figure
3.
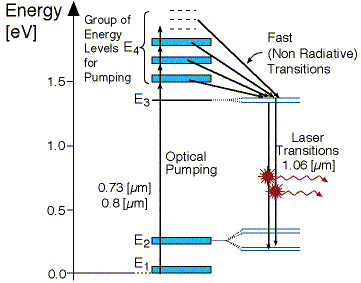
As seen in Figure 3 above, there is four energy levels, with energies
E1, E2, E3, E4 with populations of N1, N2, N3, N4 respectively. There energies
increase for each level so that E1 < E2 < E3 < E4.
In this system, optical pumping from the ground state (E1) into the pump
band (E4) excites the atoms. From this level the atoms decay by a fast,
radiationless transition into the level 3 (E3). The lifetime of the laser
transition from E3 – E2 is long compared to that of E4 –E3, a population
accumulates in this level 3 (lasing level). Here the atoms relax and start to
create laser transitions through spontaneous and stimulated emissions into level
2 (E2). At this level, like level 4 has a fast decay into the ground state. Like
before this quickly de-excited atom leads to a negligible population in E2. This
is significant, as the highly populated E3 level will then form a population
inversion with the E2 level. Specifically as long as the population of level3 N3
is greater then 0. Therefore optical amplification and laser operation can take
place.
Since only a small number of atoms need to be excited in the upper
lasing level E3 to form population inversion, it proves that a 4 level laser is
much more efficient and practical then the 3 level laser.
dN4
=
Wp(N1 – N4) – (γ43 + γ42 + γ41)N4
dt
=
Wp(N1
– N4)
– N4
τ4
dN3
= γ43*N4
- (γ32 + γ31)N3 = N4 – N3
dt
τ43 τ31
dN2 =
γ42N4
+ γ32N3 + γ21N2 = N4 + N3 –
N3
dt
τ42 τ32
τ21
Pumping
into level 3 is irrelevant due to weak absorption and narrow band.
Steady-State:
N3 = τ3
*N4
τ43
N2 =
τ21 +
τ43τ21
*N3
= βN3
τ32
τ42τ3
β
= N2
= τ21 +
τ43 τ21
N3
τ32
τ42τ3